Images taken from the Claridge Hotel/Casino rule book.
The Mathematics of Sic Bo
By
Michael Shackleford
January 21, 2005
Sic Bo, meaning "dice pair" is an ancient Chinese gambling game. Today it is one of the lesser known casino games and is often confined to designated rooms for Asian games. The game uses three dice and a table with a variety of betting options on the roll of those dice. The odds and table layout may also vary from place to place. If you must play Sic Bo I would suggest sticking to only the 'low' and 'high' bets.
Following is a list of the bets available. The payoffs listed are for Atlantic City and the Mirage in Las Vegas. Other casinoís odds will vary.
The critical step in calculating the odds in Sic Bo is to find the probability of any given total in the throw of three dice. Following is a formula for s spots over n dice, taken from The Theory of Gambling and Statistical Logic by Richard A. Epstein, formula 5-14.
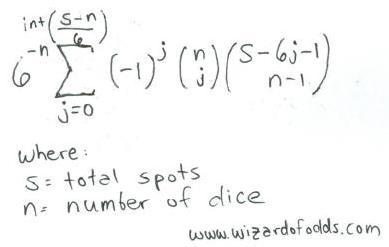
For example, let's look at the number of ways to get 11 spots over 3 dice.
int[(s-n)/6] = int[(11-3)/6] = int[1.33] = 1
The total would be 6-3 * [-10*combin(3,0)*combin(11-6*0-1,3-1) + -11*combin(3,1)*combin(11-6*1-1,3-1) ] =
1/218 * [1*1*combin(10,2) + -1*3*combin(4,2)] =
1/218 * [1*1*45 + -1*3*6] =
1/218 * [45-18] = 27/216 = 12.50%
Alternatively, if you can program a computer that would probably be the fastest way to get the results.
Here is a simple function in C++.
void SicBo(void)
{
int i,d1,d2,d3,tot,tot_array[19];
for (i=0; i<=18; i++)
tot_array[i]=0;
for (d1=1; d1<=6; d1++)
{
for (d2=1; d2<=6; d2++)
{
for (d3=1; d3<=6; d3++)
{
tot=d1+d2+d3;
tot_array[tot]++;
}
}
}
cout << "Total\tCombinations\tProbability\n";
for (i=3; i<=18; i++)
cout << i << "\t" << tot_array[i] << "\t" << (float)tot_array[i]/216 << "\n";
}
Following is the output of the function.
|
Total |
Permutations |
Probability |
|
3 |
1 |
0.00463 |
|
4 |
3 |
0.013889 |
|
5 |
6 |
0.027778 |
|
6 |
10 |
0.046296 |
|
7 |
15 |
0.069444 |
|
8 |
21 |
0.097222 |
|
9 |
25 |
0.115741 |
|
10 |
27 |
0.125 |
|
11 |
27 |
0.125 |
|
12 |
25 |
0.115741 |
|
13 |
21 |
0.097222 |
|
14 |
15 |
0.069444 |
|
15 |
10 |
0.046296 |
|
16 |
6 |
0.027778 |
|
17 |
3 |
0.013889 |
|
18 |
1 |
0.00463 |
If you donít know how to program youíre going to have to do this the hard way. What I recommend is list every combination of 3 dice. To avoid the list being 63=216 items long do not repeat the same combinations in different orders. In the interests of not listing the same number twice always order each combination from lowest to highest, not forgetting combinations with a pair or three of a kind.
So we start with 1,1,1.
Next would be 1,1,2.
Then 1,1,3; 1,1,4; 1,1,5; and 1,1,6.
Obviously you canít roll a 7 with one dice so next we increment the second die.
1,2,?
The third die must be greater or equal to the second die so the next combination in full would be 1,2,2.
Next comes 1,2,3; 1,2,4; 1,2,5; and 1,2,6.
Then comes 1,3,3.
I hope you see the pattern. The whole list would look like the following.
|
Low die |
Medium Die |
High Die |
|
1 |
1 |
1 |
|
1 |
1 |
2 |
|
1 |
1 |
3 |
|
1 |
1 |
4 |
|
1 |
1 |
5 |
|
1 |
1 |
6 |
|
1 |
2 |
2 |
|
1 |
2 |
3 |
|
1 |
2 |
4 |
|
1 |
2 |
5 |
|
1 |
2 |
6 |
|
1 |
3 |
3 |
|
1 |
3 |
4 |
|
1 |
3 |
5 |
|
1 |
3 |
6 |
|
1 |
4 |
4 |
|
1 |
4 |
5 |
|
1 |
4 |
6 |
|
1 |
5 |
5 |
|
1 |
5 |
6 |
|
1 |
6 |
6 |
|
2 |
2 |
2 |
|
2 |
2 |
3 |
|
2 |
2 |
4 |
|
2 |
2 |
5 |
|
2 |
2 |
6 |
|
2 |
3 |
3 |
|
2 |
3 |
4 |
|
2 |
3 |
5 |
|
2 |
3 |
6 |
|
2 |
4 |
4 |
|
2 |
4 |
5 |
|
2 |
4 |
6 |
|
2 |
5 |
5 |
|
2 |
5 |
6 |
|
2 |
6 |
6 |
|
3 |
3 |
3 |
|
3 |
3 |
4 |
|
3 |
3 |
5 |
|
3 |
3 |
6 |
|
3 |
4 |
4 |
|
3 |
4 |
5 |
|
3 |
4 |
6 |
|
3 |
5 |
5 |
|
3 |
5 |
6 |
|
3 |
6 |
6 |
|
4 |
4 |
4 |
|
4 |
4 |
5 |
|
4 |
4 |
6 |
|
4 |
5 |
5 |
|
4 |
5 |
6 |
|
4 |
6 |
6 |
|
5 |
5 |
5 |
|
5 |
5 |
6 |
|
5 |
6 |
6 |
|
6 |
6 |
6 |
Next we have to determine the number of permutations of each combination. A combination is a set without regard to order and a permutation is a set with regard to order.
With a three of a kind there is only one way permutation. For example if the three dice are 1,1,1 there is only one way to roll that a 1 each time.
If the combination is 1,1,2 there are three ways to roll that: 1,1,2; 1,2,1; and 2,1,1.
If all three dice are 1,2,3 there are six possible permutations: 1,2,3; 1,3,2; 2,1,3; 2,3,1; 3,1,2; 3,2,1
The general formula is that if you have a total of d dice and the totals of each number are x1, x2, x3Öxn then the number of permutations are d!/(x1!*x2!*x3*Ö*xn). So the number of ways to get a three of a kind would be 3!/3! = 6/6 = 1. The number of ways to get a pair would be 3!/(2!*1!) = 6/(2*1) = 3. The number of ways to get three different numbers would be 3!/(1!*1!*1!) = 6/(1*1*1) = 6.
|
Low die |
Medium die |
High die |
Total |
Permutations |
|
1 |
1 |
1 |
3 |
1 |
|
1 |
1 |
2 |
4 |
3 |
|
1 |
1 |
3 |
5 |
3 |
|
1 |
1 |
4 |
6 |
3 |
|
1 |
1 |
5 |
7 |
3 |
|
1 |
1 |
6 |
8 |
3 |
|
1 |
2 |
2 |
5 |
3 |
|
1 |
2 |
3 |
6 |
6 |
|
1 |
2 |
4 |
7 |
6 |
|
1 |
2 |
5 |
8 |
6 |
|
1 |
2 |
6 |
9 |
6 |
|
1 |
3 |
3 |
7 |
3 |
|
1 |
3 |
4 |
8 |
6 |
|
1 |
3 |
5 |
9 |
6 |
|
1 |
3 |
6 |
10 |
6 |
|
1 |
4 |
4 |
9 |
3 |
|
1 |
4 |
5 |
10 |
6 |
|
1 |
4 |
6 |
11 |
6 |
|
1 |
5 |
5 |
11 |
3 |
|
1 |
5 |
6 |
12 |
6 |
|
1 |
6 |
6 |
13 |
3 |
|
2 |
2 |
2 |
6 |
1 |
|
2 |
2 |
3 |
7 |
3 |
|
2 |
2 |
4 |
8 |
3 |
|
2 |
2 |
5 |
9 |
3 |
|
2 |
2 |
6 |
10 |
3 |
|
2 |
3 |
3 |
8 |
3 |
|
2 |
3 |
4 |
9 |
6 |
|
2 |
3 |
5 |
10 |
6 |
|
2 |
3 |
6 |
11 |
6 |
|
2 |
4 |
4 |
10 |
3 |
|
2 |
4 |
5 |
11 |
6 |
|
2 |
4 |
6 |
12 |
6 |
|
2 |
5 |
5 |
12 |
3 |
|
2 |
5 |
6 |
13 |
6 |
|
2 |
6 |
6 |
14 |
3 |
|
3 |
3 |
3 |
9 |
1 |
|
3 |
3 |
4 |
10 |
3 |
|
3 |
3 |
5 |
11 |
3 |
|
3 |
3 |
6 |
12 |
3 |
|
3 |
4 |
4 |
11 |
3 |
|
3 |
4 |
5 |
12 |
6 |
|
3 |
4 |
6 |
13 |
6 |
|
3 |
5 |
5 |
13 |
3 |
|
3 |
5 |
6 |
14 |
6 |
|
3 |
6 |
6 |
15 |
3 |
|
4 |
4 |
4 |
12 |
1 |
|
4 |
4 |
5 |
13 |
3 |
|
4 |
4 |
6 |
14 |
3 |
|
4 |
5 |
5 |
14 |
3 |
|
4 |
5 |
6 |
15 |
6 |
|
4 |
6 |
6 |
16 |
3 |
|
5 |
5 |
5 |
15 |
1 |
|
5 |
5 |
6 |
16 |
3 |
|
5 |
6 |
6 |
17 |
3 |
|
6 |
6 |
6 |
18 |
1 |
|
Total |
216 |
Next we go through the tedious process of adding the number of permutations for each total. For example a total of 6 has the following combinations with the corresponding number of permutations.
|
Combinations |
Number of Permutations |
|
1,1,4 |
3 |
|
1,2,3 |
6 |
|
2,2,2 |
1 |
|
Total |
10 |
The final table will look like this, not unlike the result of the computer function earlier.
So now lets add a column to our list for the number of combinations of each set. Letís also add a total for the three dice.
|
Total |
Permutations |
|
3 |
1 |
|
4 |
3 |
|
5 |
6 |
|
6 |
10 |
|
7 |
15 |
|
8 |
21 |
|
9 |
25 |
|
10 |
27 |
|
11 |
27 |
|
12 |
25 |
|
13 |
21 |
|
14 |
15 |
|
15 |
10 |
|
16 |
6 |
|
17 |
3 |
|
18 |
1 |
|
Total |
216 |
Now we can divide each total number permutations by the total number 3-dice permutations (216) to get the probability of each total.
|
Total |
Permutations |
Probability |
|
3 |
1 |
0.00463 |
|
4 |
3 |
0.013889 |
|
5 |
6 |
0.027778 |
|
6 |
10 |
0.046296 |
|
7 |
15 |
0.069444 |
|
8 |
21 |
0.097222 |
|
9 |
25 |
0.115741 |
|
10 |
27 |
0.125 |
|
11 |
27 |
0.125 |
|
12 |
25 |
0.115741 |
|
13 |
21 |
0.097222 |
|
14 |
15 |
0.069444 |
|
15 |
10 |
0.046296 |
|
16 |
6 |
0.027778 |
|
17 |
3 |
0.013889 |
|
18 |
1 |
0.00463 |
|
Total |
216 |
1 |
Finally, we are ready to evaluate the expected value of each bet. The expected value is the ratio of the amount the player can expect to win to the amount he bets on any given bet. So a fair bet would an expected value of zero. A positive expected value would mean the player has the advantage. A negative expected value would mean the dealer has the advantage.
Letís start with the 4 bet. This wins with a total of 4 and pays 60 to 1. For those who donít know, "60 to 1" means if the player wins he wins 60 times his bet and KEEPS his original wager. Had the odds paid "60 for 1" the player would NOT keep his original bet. Most table games pay on a "to 1" basis.
The probability of a total of 4 is 3/216 = 0.013889. Thus the probability of losing is 1-(3/216) = 1-0.013889 = 0.986111.
The expected value of any bet with only two possibilities, winning or losing, is:
(Probability of winning)*(Amount of win) + (Probability of losing)*(Amount of loss).
For the 4 bet the expected value is
0.013889 * 60 - 0.986111*-1 = -0.15278.
So, this tells us that for every dollar the player bets on a total of 4 he can expect to lose 15.278 cents on average. Or, the house edge is 15.278%.
The next table shows the expected value and how it was calculated for all bets of a total of 4 to 17.
|
Total |
Pays |
Probability of Win |
Probability of Losing |
Formula of expected value |
Expected Value |
|
4 |
60 |
0.013889 |
0.986111 |
0.0138889*60-0.986111*-1 |
-0.15278 |
|
5 |
30 |
0.027778 |
0.972222 |
0.0277778*30-0.972222*-1 |
-0.13889 |
|
6 |
17 |
0.046296 |
0.953704 |
0.0462963*17-0.953704*-1 |
-0.16667 |
|
7 |
12 |
0.069444 |
0.930556 |
0.0694444*12-0.930556*-1 |
-0.09722 |
|
8 |
8 |
0.097222 |
0.902778 |
0.0972222*8-0.902778*-1 |
-0.125 |
|
9 |
6 |
0.115741 |
0.884259 |
0.115741*6-0.884259*-1 |
-0.18981 |
|
10 |
6 |
0.125 |
0.875 |
0.125*6-0.875*-1 |
-0.125 |
|
11 |
6 |
0.125 |
0.875 |
0.125*6-0.875*-1 |
-0.125 |
|
12 |
6 |
0.115741 |
0.884259 |
0.115741*6-0.884259*-1 |
-0.18981 |
|
13 |
8 |
0.097222 |
0.902778 |
0.0972222*8-0.902778*-1 |
-0.125 |
|
14 |
12 |
0.069444 |
0.930556 |
0.0694444*12-0.930556*-1 |
-0.09722 |
|
15 |
17 |
0.046296 |
0.953704 |
0.0462963*17-0.953704*-1 |
-0.16667 |
|
16 |
30 |
0.027778 |
0.972222 |
0.0277778*30-0.972222*-1 |
-0.13889 |
|
17 |
60 |
0.013889 |
0.986111 |
0.0138889*60-0.986111*-1 |
-0.15278 |
Two of a kind
There are combin(6,2)=6!/(4!*2!)=15 ways to choose two numbers out of six. Each of these combinations is listed on the table and the player bet on as many as he wishes. If both numbers appear on the roll of the three dice then the player wins and is paid 15 to 1.
Letís assume the player picks a 1 and 2 as his two numbers. What is the probability that both a 1 and 2 occur in the roll of 3 dice? One way to do this would be to note all the possible winning permutations:
|
Dice |
Number of Permutations |
|
1,2,3 |
6 |
|
1,2,4 |
6 |
|
1,2,5 |
6 |
|
1,2,6 |
6 |
|
1,1,2 |
3 |
|
1,2,2 |
3 |
|
Total |
30 |
Thus there are a total of 30 winning permutations.
There are 63=216 total permutations, so the probability of winning is 30/216 = 1/36 = 0.1388889
The two of a kind bet pays 5 to 1. So the expected value is 0.1388889*5 + (1-0.1388889)*-1 = -0.16667. In other words the house edge is 16.67%.
Double
There are six double bets available, one for each number from 1 to 6. The player may be on any one or combination of bets. Any given bet wins if at least two of the three dice land on that number.
Letís assume the player bets on the 1.
One way to solve it would be to note all the winning permutations:
|
Dice |
Number of Permutations |
|
1,1,2 |
3 |
|
1,1,3 |
3 |
|
1,1,4 |
3 |
|
1,1,5 |
3 |
|
1,1,6 |
3 |
|
1,1,1 |
1 |
|
Total |
16 |
Thus there are a total of 16 winning permutations.
There are 63=216 total permutations, so the probability of winning is 16/216 = 0.0740741.
The double bet pays 10 to 1. So the expected value is 0.0740741*10 + (1-0.0740741)*-1 = -0.18518. In other words the house edge is 18.52% (ouch!).
Triple
Player may bet on any specific number (for example a 1). Player wins if all 3 dice land on that number.
There is obviously only one way to win this bet, so the probability of winning is 1/216 = 0.0046296. The bet pays 180 to 1 so the expected value is 0.0046296*180 + (1-0.0046296)*-1 = -0.16204. So the house edge is 16.204%.
Any Triple
The Any Triple bet pays if any three of a kind is thrown. There are obviously six winning combinations (1,1,1; 2,2,2; 3,3,3; etc.). So the probability of winning is 6/216 = 0.027778. The bet pays 30 to 1 so the expected value is 0.027778*30 + (1-0.027778)*-1 = -0.13889. So the house edge is 13.89%.
Low
The low bet wins if the total of the three dice is 3 to 10, without being a three of a kind. The probability of any total 10 or less is exactly 50%. The average number on any one die is (1+2+3+4+5+6)/6 = 21/6 = 3.5. So the average of three dice is 3*3.5 = 10.5. It stands to reason that the probability of getting under or over 10.5 is 50%.
However the bet loses on a three of a kind. There are 3 three of a kinds that would turn a winner into a loser: 1,1,1; 2,2,2; and 3,3,3. So the probability of having a total of 10 or less as a three of a kind is 3/216 = 0.0188889. So the overall probability of winning is 0.5 Ė 0.188889 = 0.4861111. The bet pays 1 to 1 so the expected value is 0.4861111*1 + (1-0.4861111)*-1 = -0.02778. Thus the house edge is 2.78%.
High
The high is just the opposite of the low bet, so it stands to reason the house edge would also be 2.78%.
Individual Number
Player may bet on any specific number from 1 to 6. If chosen number appears 1 time bet pays 1 to 1, if it appears 2 times bet pays 2 to 1, and if it appears 3 times it pays 3 to 1. Probability of 1 match is 34.72%, 2 matches is 6.94%, 3 matches is 0.46%.
Letís assume the player picks the number one.
There is only one way to get three ones: 1,1,1. So the probability of three ones is 1/63 = 1/216.
Following are the ways to get two 1ís and the number of permutations of each.
|
Dice |
Number of Permutations |
|
1,1,2 |
3 |
|
1,1,3 |
3 |
|
1,1,4 |
3 |
|
1,1,5 |
3 |
|
1,1,6 |
3 |
|
Total |
15 |
So the probability of two ones is 15/63 = 15/216.
Following are the ways to get one 1 and the number of permutations of each.
|
Dice |
Number of Permutations |
|
1,2,2 |
3 |
|
1,2,3 |
6 |
|
1,2,4 |
6 |
|
1,2,5 |
6 |
|
1,2,6 |
6 |
|
1,3,3 |
3 |
|
1,3,4 |
6 |
|
1,3,5 |
6 |
|
1,3,6 |
6 |
|
1,4,4 |
3 |
|
1,4,5 |
6 |
|
1,4,6 |
6 |
|
1,5,5 |
3 |
|
1,5,6 |
6 |
|
1,6,6 |
3 |
|
Total |
75 |
So the probability of two ones is 75/63 = 75/216.
Another way to arrive at the probability of one 1 would be find the probability that the first die is a one and the second and third are not:
Pr(one)*Pr(not one)*Pr(not one) = (1/6)*(5/6)*(5/6) = 25/216.
However the one could appear in the first, second, or third position, so multiply by 3: 3*(25/216) = 75/216.
The probability of rolling zero ones is Pr(not one)*Pr(not one)*Pr(not one) = (5/6)*(5/6)*(5/6) = (5/6)3 = 125/216.
The following return table shows the possible outcomes, and the number of combinations, probability, and return of each. The return is the product of the probability and the win or loss to the player.
|
Event |
Permutations |
Probability |
Pays |
Return |
|
Player rolls 3 ones |
1 |
0.00463 |
3 |
0.013889 |
|
Player rolls 2 ones |
15 |
0.069444 |
2 |
0.138889 |
|
Player roll 1 one |
75 |
0.347222 |
1 |
0.347222 |
|
Player rolls 0 ones |
125 |
0.578704 |
-1 |
-0.5787 |
|
Total |
216 |
1 |
-0.0787 |
So the total expected return is -0.0787, or the house edge is 7.87%.
Sic Bo section at the Wizard of Odds.
How to calcualte the 3-dice permutation in Visual Basic.